 .
.



Cette thèse a pour objet la classification - à isotopie près - des fonctions rationnelles réel-étales de.
Une fonction rationnelle réelle est une fraction de deux polynômes à coefficients réels, ou, de manière équivalente, un morphisme de
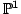 dans lui-même. Une telle fonction est dite réel-étale si elle n'a pas de ramification au-dessus des points réels. Comme nous le verrons plus bas, ces fonctions sont intéressantes à cause de leur lien avec les M-surfaces. Notre étude fait aussi le pendant de l'article [EG02] de A. Eremenko et A. Gabrielov dans lequel ils résolvent une conjecture de B. et M. Shapiro en dimension 1. Pour cela, ils étudient les fonctions rationnelles sur
dans lui-même. Une telle fonction est dite réel-étale si elle n'a pas de ramification au-dessus des points réels. Comme nous le verrons plus bas, ces fonctions sont intéressantes à cause de leur lien avec les M-surfaces. Notre étude fait aussi le pendant de l'article [EG02] de A. Eremenko et A. Gabrielov dans lequel ils résolvent une conjecture de B. et M. Shapiro en dimension 1. Pour cela, ils étudient les fonctions rationnelles sur
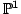 dont tous les points de ramification sont réels.
dont tous les points de ramification sont réels.
Si on regardait les fonctions rationnelles réel-étales à homotopie près, on pourrait passer par des fonctions rationnelles ramifiées au-dessus des points réels. Cette classification est trop grossière. C'est pourquoi nous étudions plutôt les fonctions rationnelles réel-étales à isotopie près. Deux fonctions rationnelles réel-étales sont isotopes si l'on peut passer de l'une à l'autre par déformation continue dans l'ensemble des fonctions rationnelles réel-étales de même degré.
Pour définir de façon précise cette notion d'isotopie, une première partie de ma thèse développe la théorie des familles continues de surfaces de Klein. Pour cela, j'utilise le point de vue des espaces localement annelés. Ils permettent entre autre une définition plus naturelle des morphismes de surfaces de Klein que celle de la théorie classique. D'autre part, ils facilitent le travail en famille. Lors de cette étude, je démontre aussi un Théorème d'Existence de Riemann pour ces familles.
Les principaux objets qui interviennent dans la classification sont les arbres signés associés à une fonction rationnelle réel-étale. Topologiquement, un endomorphisme de
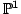 est un revêtement ramifié du disque fermé par lui-même. Une fonction rationnelle
est un revêtement ramifié du disque fermé par lui-même. Une fonction rationnelle 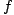 sur
sur
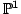 est réel-étale si et seulement si l'image réciproque
est réel-étale si et seulement si l'image réciproque
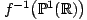 des points réels est la réunion disjointe de cercles topologiques dans
des points réels est la réunion disjointe de cercles topologiques dans
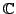 .
.
Ces cercles sont les arêtes de l'arbre. Les sommets de l'arbre sont les composantes connexes de
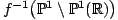 . Un sommet s est l'extrémité d'une arête e si le cercle topologique e est inclus dans l'adhérence de s dans
. Un sommet s est l'extrémité d'une arête e si le cercle topologique e est inclus dans l'adhérence de s dans
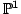 .
De plus, l'arbre est pondéré: à chaque arête e est associé le degré topologique de
.
De plus, l'arbre est pondéré: à chaque arête e est associé le degré topologique de 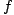 restreint à e . Une orientation sur
restreint à e . Une orientation sur
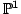 induit une orientation sur ses points réels. On ajoute alors au pied de l'arbre de
induit une orientation sur ses points réels. On ajoute alors au pied de l'arbre de 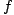 un signe "+" ou "-" selon que
un signe "+" ou "-" selon que 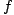 préserve ou inverse respectivement l'orientation sur
préserve ou inverse respectivement l'orientation sur
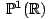 . Ceci donne l'arbre signé de
. Ceci donne l'arbre signé de 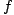 .
.
Réciproquement, on montre que tout arbre signé peut être associé à une fonction rationnelle réel-étale.
Nous pouvons maintenant énoncer le résultat au coeur de ma thèse:


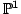 :
:
La partie la plus délicate de la démonstration consiste à montrer la réciproque, c'est-à-dire obtenir une isotopie entre deux fonctions rationnelles réel-étales 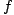 et
et 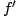 ayant même arbre signé. Elle repose sur les trois idées suivantes.
ayant même arbre signé. Elle repose sur les trois idées suivantes.
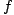 et
et 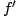 , on peut supposer qu'il s'agit de revêtements ramifiés génériques, c'est à dire tels que chaque fibre pour
, on peut supposer qu'il s'agit de revêtements ramifiés génériques, c'est à dire tels que chaque fibre pour 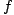 ou
ou 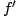 admette au plus un point de ramification et tels que tous ces points de ramification soient des points doubles.
admette au plus un point de ramification et tels que tous ces points de ramification soient des points doubles.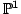 préservant l'orientation est isotope à l'identité. Ceci permet d'affirmer que tout couple d'homéomorphismes
préservant l'orientation est isotope à l'identité. Ceci permet d'affirmer que tout couple d'homéomorphismes 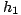 et
et 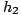 de
de
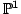 faisant commuter le diagramme
faisant commuter le diagramme ![$\displaystyle \xymatrix{\mathbb P^{\smash{1}}\ar[rr]^{h_{2}}\ar[d]_{f}&&\mathbb...
...{1}}\ar[d]^{f'}\\
\mathbb P^{\smash{1}}\ar[rr]^{h_{1}}&&\mathbb P^{\smash{1}}}$](Resume/img18.png) induit une isotopie entre
induit une isotopie entre 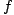 et
et 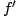 .
.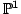 le long des composantes connexes de
le long des composantes connexes de
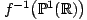 d'une part et le long des composantes connexes de
d'une part et le long des composantes connexes de
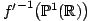 d'autre part. Ceci permet de nous ramener à des revêtements réel-étales génériques strictes de
d'autre part. Ceci permet de nous ramener à des revêtements réel-étales génériques strictes de
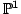 par des variétés homéomorphes à un disque fermé privé de disques ouverts disjoints. Une étude des systèmes de Hurwitz associés à de tels revêtements va permettre de trouver un homéomorphisme préservant l'orientation
par des variétés homéomorphes à un disque fermé privé de disques ouverts disjoints. Une étude des systèmes de Hurwitz associés à de tels revêtements va permettre de trouver un homéomorphisme préservant l'orientation
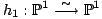
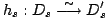
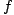 et
et 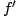 à un même sommet s de leur arbre. Tout est fait en sorte que les homéomorphismes
à un même sommet s de leur arbre. Tout est fait en sorte que les homéomorphismes 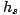 puissent se recoller pour former l'homéomorphisme
puissent se recoller pour former l'homéomorphisme 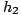 de
de
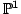 cherché précédemment (voir Idée 2).
cherché précédemment (voir Idée 2).

Le théorème de classification des fonctions rationnelles réel-étales de
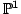 s'applique à l'étude de l'espace de module des M -courbes algébriques réelles de genre g ou, pour rester dans la catégorie des surfaces de Klein, des M -surfaces de genre g . En effet, il se trouve que cet espace plutôt mystérieux est caché dans l'espace des fonctions rationnelles réel-étales de degré 2g+1 .
s'applique à l'étude de l'espace de module des M -courbes algébriques réelles de genre g ou, pour rester dans la catégorie des surfaces de Klein, des M -surfaces de genre g . En effet, il se trouve que cet espace plutôt mystérieux est caché dans l'espace des fonctions rationnelles réel-étales de degré 2g+1 .
En effet, soit 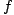 une fonction rationnelle réel-étale de degré d=2g+1 sur
une fonction rationnelle réel-étale de degré d=2g+1 sur
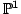 , dont l'arbre est de la forme
, dont l'arbre est de la forme
![$\displaystyle \xymatrix @M=0pt{
\bullet & \ar@/^2pt/@{.}[rr]^{g\text{ cotés}}_{...
... \bullet\\
&& \ar@{-}[ull]^{1} \bullet \ar@{-}[urr]_{1} \\
&&\ar@{-}[u]^{1}
}$](Resume/img26.png)
c'est à dire pour lequel tous les côtés ont pour poids 1 et qui a le maximum de sommets rencontrant une seule branche. Un tel arbre est appelé M -arbre et 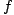 est appelé un M -endomorphisme. On peut associer de façon naturelle à
est appelé un M -endomorphisme. On peut associer de façon naturelle à 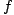 une M -surface
une M -surface 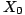 de genre g qui, topologiquement, est l'adhérence de la composante connexe de
de genre g qui, topologiquement, est l'adhérence de la composante connexe de
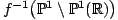 contenant
contenant
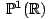 .
La M -surface
.
La M -surface 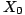 vient avec un morphisme réel-étale
vient avec un morphisme réel-étale
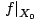 de degré g+1 et le choix particulier d'une composante connexe de son bord qui est
de degré g+1 et le choix particulier d'une composante connexe de son bord qui est
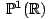 . Ainsi, on peut associer à un M-endomorphisme
. Ainsi, on peut associer à un M-endomorphisme 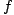 de
de
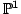 un triplet
un triplet
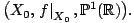 Soit
Soit
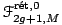 l'ensemble des fonctions rationnelles réel-étales de degré 2g+1 modulo l'action des automorphismes de
l'ensemble des fonctions rationnelles réel-étales de degré 2g+1 modulo l'action des automorphismes de
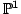 par composition à droite. Cet espace admet une structure naturelle de variété analytique réelle. Soit
par composition à droite. Cet espace admet une structure naturelle de variété analytique réelle. Soit
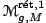 l'ensemble des classes d'isomorphismes de triplets
l'ensemble des classes d'isomorphismes de triplets 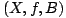 tels que
tels que 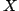 soit une M -surface de genre g ,
soit une M -surface de genre g , 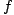 une fonction rationnelle réel-étale de degré g+1 sur
une fonction rationnelle réel-étale de degré g+1 sur 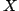 et
et 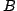 une composante connexe du bord de
une composante connexe du bord de 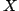 . On démontre que
. On démontre que
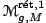 admet une structure naturelle de variété à priori semi-analytique.
admet une structure naturelle de variété à priori semi-analytique.
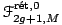 |
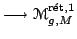 |
|
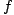 |
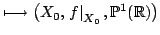 |
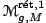 admet une structure naturelle de variété analytique réelle.
admet une structure naturelle de variété analytique réelle.
Dans le cas particulier des M-surfaces de genre 1, une étude plus concrète montre que si cet isomorphisme est naturel, il n'est pas trivial.
La démonstration du théorème précédent passe par des espaces de Teichmüller de triplets et de M-endomorphismes. Les familles analytiques réelles de surfaces de Klein interviennent aussi de manière essentielle.
Le théorème de classification des fonctions rationnelles réel-étales de
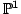 donne une démonstra-tion nouvelle de la connexité de l'espace des modules de M-surfaces de genre g , montrée par M. Seppälä et R. Silhol [SS89]. En effet,
donne une démonstra-tion nouvelle de la connexité de l'espace des modules de M-surfaces de genre g , montrée par M. Seppälä et R. Silhol [SS89]. En effet,
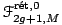 est connexe d'après le théorème de classification des fonctions rationnelles réel-étale de
est connexe d'après le théorème de classification des fonctions rationnelles réel-étale de
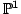 ci-dessus, et le morphisme oubli
ci-dessus, et le morphisme oubli
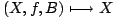 de
de
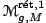 sur l'espace des modules de M-surface de genre g est une surjection analytique réelle.
sur l'espace des modules de M-surface de genre g est une surjection analytique réelle.




